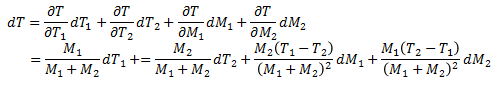CodeIQ @masuipeoさんの問題「同じ大きさに分割」を解いた。今回の問題は、m×n個のマスからなる領域を、連結な二つの領域に分割せよ、というもの。
バッジを貰えたのでソースコードを公開しておく。といってもこれはオリジナルの回答ではなくて、フィードバックを見た後で高速化のための改良を施してある。言語は例によってFortran。
!****************************************************************************
!
program divide
!
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
! 変数
integer :: l, m, n, ss, ans
integer, allocatable :: c(:)
! m : number of lows
! n : number of columns
! l = m*n
! ss : number of red
! c(0:l-1) : i-th cell's color is red if c(i) = 1
! blue if c(i) = 0
! ans : answer
read(*, *)m, n, ss
l = m*n
allocate(c(0:l-1))
ans = 0
open(11, file = 'ans.txt', status = 'unknown')
write(11, 1000)m, n, ss
1000 format('# m, n, ss = ', 3(1x, i3))
c=0
c(0)=1
call gen(l, m, n, ss, c, 0, 1, ans)
write(11, 1100)ans
write(nstde, 1100)ans
1100 format('# ans = ', i6)
end program divide
!****************************************************************************
recursive subroutine gen(l, m, n, ss, c, r, s, ans)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: l, m, n, ss
integer, intent(inout) :: c(0:l-1)
integer, intent(in) :: r, s
integer, intent(inout) :: ans
integer :: i
if(l-1-r < ss-s)then
return
elseif(s == ss)then
call check(l, m, n, ss, c, ans)
else
do i = r+1, l-1
c(r+1:l-1) = 0
c(i) = 1
call gen(l, m, n, ss, c, i, s+1, ans)
enddo
endif
end subroutine gen
!****************************************************************************
subroutine check(l, m, n, ss, c, ans)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: l, m, n, ss, c(0:l-1)
integer, intent(inout) :: ans
integer :: d(0:l)
! d : 連結かどうかを調べる為の一時領域
integer :: i, j, k, kk
d = 0
d(0) = 1
do k = 1, l-1
if(c(k) == 0)then
d(k) = 1
exit
endif
enddo
do kk = 1, max(ss, l-ss)
do k = 0, l-1
if(mod(k, n) > 0)then
if(c(k-1) == c(k) .and. d(k-1) == 1)d(k) = 1
endif
if(mod(k, n) < n-1)then
if(c(k+1) == c(k) .and. d(k+1) == 1)d(k) = 1
endif
if(k/n > 0)then
if(c(k-n) == c(k) .and. d(k-n) == 1)d(k) = 1
endif
if(k/n < m-1)then
if(c(k+n) == c(k) .and. d(k+n) == 1)d(k) = 1
endif
enddo
enddo
if(sum(d) == l)then
ans = ans+1
do i = 0, m-1
write(11, 1000) (c(i*n+j), j = 0, n-1)
1000 format(100(1x, i2))
enddo
write(11, *)
endif
end subroutine check
2014年6月11日水曜日
2014年6月7日土曜日
魔方陣(CodeIQ)
CodeIQで、Short Coder @ozy4dm Ozyさんの出題「魔方陣ヌルヌル」を解いた。1列の和が0となることを除いては普通の魔方陣とルールは同じ。
連立一次方程式に帰着して力技で解くことにした。理由は、魔方陣の解き方について全く知らなかったこと(効率的に空白を埋めていく方法があるらしい)と、連立一次方程式の解法について復習したかったから。
求め方は、まず各マスに番号を振る。たとえば3×3の魔方陣の場合はこんな感じ。
それぞれのマスに入る数字をx(1)…x(n^2)とすると、以下のようなn^2元連立一次方程式を立てることができる。
x(1)+x(2)+…x(n)=0
x(n+1)+x(n+2)+…+x(2n)=0
…
x(n(n-1)+1)+x(n^2-n+2)+…+x(n^2)=0
x(1)+x(n+1)+…+x(n(n-1)+1)=0
x(2)+x(n+2)+…+x(n(n-1)+2)=0
…
x(n)+x(2n)+…+x(n^2)=0
x(1)+x(n+2)+…+x(n^2)=0
x(n)+x(2n-1)+…+x(n(n-1)+1)=0
これを2n+2行n^2列の行列Aを用いてAx=0としてガウス・ジョルダン法で解く。ただし、rank(A)=n^2にはならない。ちゃんと確認していないがrank(A)=2n+1になるもよう。rank(A)≠n^2のとき解はn^2-rank(A)個の未知のパラメータを含むので、このパラメータをx(1)…x(n^2)適当に選ぶ。
解き方は以上だが、魔方陣の場合は各数字が整数であるという制約があるので、ガウス・ジョルダン法をそのまま適用するのではなく、手順の途中で小数が入り込まないように工夫する必要がある。また、パラメータも解が整数になるように選ぶ必要がある(本来はちゃんと探索するべきだろうけど今回は適当に決めたらうまくいったのでプログラム中では決め打ちになっている)。
以下ソースコード。使用言語はFortran。前進消去と交代代入を別のプログラムにした。
ソースコード1(ガウス・ジョルダン法の前進消去までを行う)
!****************************************************************************
!
program msquare1
!
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
! 変数
integer :: m
! m : 魔方陣のサイズ(1辺に含まれる数字の個数)
integer, allocatable :: a(:,:), b(:), x(:)
! a(2*m+2,m**2) : 連立一次方程式の係数
! b(2*m+2) : 連立一次方程式の右辺
! x(m**2) : 解(1次元表記)
!
! 1次元配列xと魔方陣yの関係
! x(k) = y(i, j)
! k = (i-1)*m+j
! i = k/m+1
! j = mod(k,m)
integer, allocatable :: ix(:)
integer :: rank
! ix(m**2) : 列の入れ替え情報
! rank : 行列のランク
character(len=100) :: ofile
! ofile : 出力ファイル名
integer :: io
write(nstde, *)'# m = ?'
read(*, *)m
allocate(a(2*m+2, m**2), b(2*m+2), x(2*m+2))
! --- a, bを生成する ---
call struct_a(m, a)
! b = (m**2)*(m**2+1)/2/m ! 普通の魔方陣の条件
b = 0 ! ヌルヌルした魔方陣の条件(右辺=0)
write(nstde, *)'# --- a ---'
call print_mat(nstde, 2*m+2, m**2, a)
write(nstde, *)'# --- b ---'
call print_mat(nstde, 2*m+2, 1, b)
write(nstde, *)'# processing...'
! aのランクを求める
allocate(ix(m**2))
call calc_rank(2*m+2, m**2, a, b, ix, rank)
! 結果を出力する
write(ofile, 1000)m
1000 format('matrix',i2.2,'.txt')
open(11, file = trim(ofile), status = 'unknown', iostat = io)
if(io /= 0)then
write(nstde, *)'# can not open ' // trim(ofile) // '.'
stop
endif
write(11, *)'# --- m ---'
write(11, *) m
write(11, *)'# --- rank ---'
write(11, *) rank
write(11, *)'# --- a ---'
call print_mat(11, 2*m+2, m**2, a)
write(11, *)'# --- b ---'
call print_mat(11, 2*m+2, 1, b)
write(11, *)'# --- ix ---'
call print_mat(11, m**2, 1, ix)
close(11)
write(nstde, *)'# --- m ---'
write(nstde, *) m
write(nstde, *)'# --- rank ---'
write(nstde, *) rank
write(nstde, *)'# --- a ---'
call print_mat(nstde, 2*m+2, m**2, a)
write(nstde, *)'# --- b ---'
call print_mat(nstde, 2*m+2, 1, b)
write(nstde, *)'# --- ix ---'
call print_mat(nstde, m**2, 1, ix)
end program msquare1
!****************************************************************************
subroutine struct_a(m, a)
!****************************************************************************
implicit none
integer, intent(in) :: m
integer, intent(inout) :: a(2*m+2, m**2)
integer :: i, j, k
! --- 初期化 ---
a=0
! --- 横 ---
do i = 1, m
do j = 1, m
k = (i-1)*m+j
a(i, k) = 1
enddo
enddo
! 縦
do j = 1, m
do i = 1, m
k = (i-1)*m+j
a(j+m, k) = 1
enddo
enddo
! 斜め
do i = 1, m
k = (i-1)*m+i
a(2*m+1, k) = 1
enddo
do i = 1, m
k = (i-1)*m+(m-i+1)
a(2*m+2, k) = 1
enddo
end subroutine struct_a
!****************************************************************************
subroutine calc_rank(m, n, a, b, ix, rank)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), b(m), ix(n), rank
integer :: i, j, ii, jj, tmp
do i = 1, n
ix(i) = i
enddo
l1: do i = 1, m
do jj = i, n
do ii = i, m
if(a(ii, jj) /= 0)then
call chgrow(m, n, a, b, i, ii)
call chgcol(m, n, a, ix, i, jj)
call setcol0(m, n, a, b, i)
call normalize2(m, n, a, b)
cycle l1
endif
enddo
enddo
rank = i-1
return
enddo l1
end subroutine calc_rank
!****************************************************************************
subroutine chgrow(m, n, a, b, i1, i2)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), b(m)
integer, intent(in) :: i1, i2
integer, allocatable :: rtmp(:)
integer :: tmp
allocate(rtmp(n))
rtmp = a(i1, :)
a(i1, :) = a(i2, :)
a(i2, :) = rtmp
deallocate(rtmp)
tmp = b(i1)
b(i1) = b(i2)
b(i2) = tmp
end subroutine chgrow
!****************************************************************************
subroutine chgcol(m, n, a, ix, j1, j2)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), ix(n)
integer, intent(in) :: j1, j2
integer, allocatable :: rtmp(:)
integer :: tmp
allocate(rtmp(m))
rtmp = a(:, j1)
a(:, j1) = a(:, j2)
a(:, j2) = rtmp
deallocate(rtmp)
tmp = ix(j1)
ix(j1) = ix(j2)
ix(j2) = tmp
end subroutine chgcol
!****************************************************************************
subroutine setcol0(m, n, a, b, i)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), b(m)
integer, intent(in) :: i
integer :: ii, j, tmp
do ii = 1, m
if(ii == i)cycle
tmp = a(ii, i)
do j = 1, n
a(ii, j) = a(i, i)*a(ii,j) - tmp*a(i, j)
enddo
b(ii) = a(i, i)*b(ii) - tmp*b(i)
enddo
end subroutine setcol0
!****************************************************************************
subroutine normalize(m, n, a, x)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), x(m)
integer :: i, j
integer :: tmp, tmp2
l2:do i = 1, min(m, n)
if(a(i, i) /= 0)then
l1:do tmp2 = a(i, i), 1, -a(i, i)/abs(a(i, i))
do j = 1, n
if(mod(a(i, j), tmp2) /=0)cycle l1
enddo
if(mod(x(i), tmp2) /= 0)cycle l1
do j = 1, n
a(i, j) = a(i, j) / tmp2
enddo
x(i) = x(i) / tmp2
cycle l2
enddo l1
endif
enddo l2
end subroutine normalize
!****************************************************************************
subroutine normalize2(m, n, a, x)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), x(m)
integer :: i, j
integer :: tmp, tmp2
l2:do i = 1, m
tmp = maxval(abs(a(i,:)))
if(tmp /= 0)then
l1:do tmp2 = tmp, 1, -tmp/abs(tmp)
do j = 1, n
if(mod(a(i, j), tmp2) /=0)cycle l1
enddo
if(mod(x(i), tmp2) /= 0)cycle l1
do j = 1, n
a(i, j) = a(i, j) / tmp2
enddo
x(i) = x(i) / tmp2
cycle l2
enddo l1
endif
enddo l2
end subroutine normalize2
!****************************************************************************
subroutine print_mat(unit, m, n, a)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: unit, m, n, a(m, n)
integer :: i, j
do i = 1, m
write(unit, 1000)(a(i, j), j=1, n)
1000 format(100(1x, i4))
enddo
end subroutine print_mat
ソースコード2(ガウス・ジョルダン法の交代代入以降を行う)
!****************************************************************************
!
program msquare2
!
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
! 変数
integer :: m
! m : 魔方陣のサイズ(1辺に含まれる数字の個数)
integer, allocatable :: a(:,:), b(:), x(:), y(:,:)
! a(2*m+2,m**2) : 連立一次方程式の係数
! b(2*m+2) : 連立一次方程式の右辺
! x(m**2) : 解(1次元表示)
! y(m, m) : 解(2次元表示)
!
! 1次元配列xと魔方陣yの関係
! x(k) = y(i, j)
! k = (i-1)*m+j
! i = k/m+1
! j = mod(k,m)
integer, allocatable :: ix(:)
integer :: rank
! ix(m**2) : 列の入れ替え情報
! rank : 行列のランク
character(len=100) :: infile, ofile
! infile : msquare1の出力ファイル
integer :: i, j, io
write(nstde, *)'# infile, ofile=?'
read(*, *)infile, ofile
open(11, file = trim(infile), status = 'unknown', iostat = io)
if(io /= 0)then
write(nstde, *)'# can not open ' // trim(infile) //'.'
stop
endif
read(11, *) ! skip header
read(11, *)m
write(nstde, *)'# m=', m
allocate(a(2*m+2, m**2), b(2*m+2), x(m**2), ix(m**2))
read(11, *) ! skip header
read(11, *)rank
write(nstde, *)'# rank=', rank
read(11, *) ! skip header
do i = 1, 2*m+2
read(11, *)(a(i, j), j = 1, m**2)
enddo
write(nstde, *)'# --- a ---'
call print_mat(nstde, 2*m+2, m**2, a)
read(11, *) ! skip header
do i = 1, 2*m+2
read(11, *)b(i)
enddo
write(nstde, *)'# --- x ---'
call print_mat(nstde, 2*m+2, 1, b)
read(11, *) ! skip header
do i = 1, m**2
read(11, *)ix(i)
enddo
write(nstde, *)'# --- x ---'
call print_mat(nstde, m**2, 1, ix)
close(11)
call calc_x(2*m+2, m**2, rank, a, b, ix, x)
call check_x(m**2, x)
allocate(y(m, m))
do i = 1, m
do j = 1, m
y(i, j) = x((i-1)*m+j)
enddo
enddo
call check_y(m, y)
write(nstde, *)'# --- answer ---'
call print_mat(nstde, m, m, y)
open(12, file = trim(ofile), status = 'unknown', iostat = io)
if(io /= 0)then
write(nstde, *)'# can not open ' // trim(ofile) // '.'
stop
endif
call print_mat(12, m, m, y)
close(12)
end program msquare2
!****************************************************************************
subroutine calc_x(m, n, rank, a, b, ix, x)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, n, rank, a(m, n), b(m), ix(n)
integer, intent(out) :: x(n)
integer, allocatable :: x_tmp(:)
integer :: i, j, ii
! --- x_tmp(rank+1)~x_tmp(n)の生成(解が整数になるように適当に与える) ---
allocate(x_tmp(n))
x_tmp=0
ii = 0
do i = rank+1, n
ii = ii + 2
x_tmp(i) = ii
enddo
! --- x_tmp(1)~x_tmp(rank)の生成 ---
do i = 1, rank
x_tmp(i) = b(i)
do j = rank + 1, n
x_tmp(i) = x_tmp(i) - a(i, j) * x_tmp(j)
enddo
if(mod(x_tmp(i), a(i, i)) /= 0)then
write(nstde, *)'# not an integer.'
stop
endif
x_tmp(i) = x_tmp(i) / a(i, i)
enddo
! --- rank計算時に入れ替えていた変数を元に戻す ---
do i = 1, n
x(ix(i))=x_tmp(i)
enddo
end subroutine calc_x
!****************************************************************************
subroutine check_x(m, x)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, x(m)
integer :: i, j
do i = 1, m-1
do j = i+1, m
if(x(i) == x(j))then
write(nstde, *)i, j, x(i)
1000 format(' x(',i2,')=x(',i2,')=',i4)
endif
enddo
enddo
end subroutine check_x
!****************************************************************************
subroutine check_y(m, y)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, y(m, m)
integer :: i, j, tmp
write(nstde,*)'# --- sum ---'
do i = 1, m
write(nstde,*)sum(y(i, :))
enddo
do j = 1, m
write(nstde,*)sum(y(:, j))
enddo
tmp = 0
do i = 1, m
tmp = tmp+y(i, i)
enddo
write(nstde,*)tmp
tmp = 0
do i = 1, m
tmp = tmp+y(i, m-i+1)
enddo
write(nstde,*)tmp
end subroutine check_y
!****************************************************************************
subroutine print_mat(unit, m, n, a)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: unit, m, n, a(m, n)
integer :: i, j
do i = 1, m
write(unit, 1000)(a(i, j), j=1, n)
1000 format(100(1x, i4))
enddo
end subroutine print_mat
連立一次方程式に帰着して力技で解くことにした。理由は、魔方陣の解き方について全く知らなかったこと(効率的に空白を埋めていく方法があるらしい)と、連立一次方程式の解法について復習したかったから。
求め方は、まず各マスに番号を振る。たとえば3×3の魔方陣の場合はこんな感じ。
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
それぞれのマスに入る数字をx(1)…x(n^2)とすると、以下のようなn^2元連立一次方程式を立てることができる。
x(1)+x(2)+…x(n)=0
x(n+1)+x(n+2)+…+x(2n)=0
…
x(n(n-1)+1)+x(n^2-n+2)+…+x(n^2)=0
x(1)+x(n+1)+…+x(n(n-1)+1)=0
x(2)+x(n+2)+…+x(n(n-1)+2)=0
…
x(n)+x(2n)+…+x(n^2)=0
x(1)+x(n+2)+…+x(n^2)=0
x(n)+x(2n-1)+…+x(n(n-1)+1)=0
これを2n+2行n^2列の行列Aを用いてAx=0としてガウス・ジョルダン法で解く。ただし、rank(A)=n^2にはならない。ちゃんと確認していないがrank(A)=2n+1になるもよう。rank(A)≠n^2のとき解はn^2-rank(A)個の未知のパラメータを含むので、このパラメータをx(1)…x(n^2)適当に選ぶ。
解き方は以上だが、魔方陣の場合は各数字が整数であるという制約があるので、ガウス・ジョルダン法をそのまま適用するのではなく、手順の途中で小数が入り込まないように工夫する必要がある。また、パラメータも解が整数になるように選ぶ必要がある(本来はちゃんと探索するべきだろうけど今回は適当に決めたらうまくいったのでプログラム中では決め打ちになっている)。
以下ソースコード。使用言語はFortran。前進消去と交代代入を別のプログラムにした。
ソースコード1(ガウス・ジョルダン法の前進消去までを行う)
!****************************************************************************
!
program msquare1
!
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
! 変数
integer :: m
! m : 魔方陣のサイズ(1辺に含まれる数字の個数)
integer, allocatable :: a(:,:), b(:), x(:)
! a(2*m+2,m**2) : 連立一次方程式の係数
! b(2*m+2) : 連立一次方程式の右辺
! x(m**2) : 解(1次元表記)
!
! 1次元配列xと魔方陣yの関係
! x(k) = y(i, j)
! k = (i-1)*m+j
! i = k/m+1
! j = mod(k,m)
integer, allocatable :: ix(:)
integer :: rank
! ix(m**2) : 列の入れ替え情報
! rank : 行列のランク
character(len=100) :: ofile
! ofile : 出力ファイル名
integer :: io
write(nstde, *)'# m = ?'
read(*, *)m
allocate(a(2*m+2, m**2), b(2*m+2), x(2*m+2))
! --- a, bを生成する ---
call struct_a(m, a)
! b = (m**2)*(m**2+1)/2/m ! 普通の魔方陣の条件
b = 0 ! ヌルヌルした魔方陣の条件(右辺=0)
write(nstde, *)'# --- a ---'
call print_mat(nstde, 2*m+2, m**2, a)
write(nstde, *)'# --- b ---'
call print_mat(nstde, 2*m+2, 1, b)
write(nstde, *)'# processing...'
! aのランクを求める
allocate(ix(m**2))
call calc_rank(2*m+2, m**2, a, b, ix, rank)
! 結果を出力する
write(ofile, 1000)m
1000 format('matrix',i2.2,'.txt')
open(11, file = trim(ofile), status = 'unknown', iostat = io)
if(io /= 0)then
write(nstde, *)'# can not open ' // trim(ofile) // '.'
stop
endif
write(11, *)'# --- m ---'
write(11, *) m
write(11, *)'# --- rank ---'
write(11, *) rank
write(11, *)'# --- a ---'
call print_mat(11, 2*m+2, m**2, a)
write(11, *)'# --- b ---'
call print_mat(11, 2*m+2, 1, b)
write(11, *)'# --- ix ---'
call print_mat(11, m**2, 1, ix)
close(11)
write(nstde, *)'# --- m ---'
write(nstde, *) m
write(nstde, *)'# --- rank ---'
write(nstde, *) rank
write(nstde, *)'# --- a ---'
call print_mat(nstde, 2*m+2, m**2, a)
write(nstde, *)'# --- b ---'
call print_mat(nstde, 2*m+2, 1, b)
write(nstde, *)'# --- ix ---'
call print_mat(nstde, m**2, 1, ix)
end program msquare1
!****************************************************************************
subroutine struct_a(m, a)
!****************************************************************************
implicit none
integer, intent(in) :: m
integer, intent(inout) :: a(2*m+2, m**2)
integer :: i, j, k
! --- 初期化 ---
a=0
! --- 横 ---
do i = 1, m
do j = 1, m
k = (i-1)*m+j
a(i, k) = 1
enddo
enddo
! 縦
do j = 1, m
do i = 1, m
k = (i-1)*m+j
a(j+m, k) = 1
enddo
enddo
! 斜め
do i = 1, m
k = (i-1)*m+i
a(2*m+1, k) = 1
enddo
do i = 1, m
k = (i-1)*m+(m-i+1)
a(2*m+2, k) = 1
enddo
end subroutine struct_a
!****************************************************************************
subroutine calc_rank(m, n, a, b, ix, rank)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), b(m), ix(n), rank
integer :: i, j, ii, jj, tmp
do i = 1, n
ix(i) = i
enddo
l1: do i = 1, m
do jj = i, n
do ii = i, m
if(a(ii, jj) /= 0)then
call chgrow(m, n, a, b, i, ii)
call chgcol(m, n, a, ix, i, jj)
call setcol0(m, n, a, b, i)
call normalize2(m, n, a, b)
cycle l1
endif
enddo
enddo
rank = i-1
return
enddo l1
end subroutine calc_rank
!****************************************************************************
subroutine chgrow(m, n, a, b, i1, i2)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), b(m)
integer, intent(in) :: i1, i2
integer, allocatable :: rtmp(:)
integer :: tmp
allocate(rtmp(n))
rtmp = a(i1, :)
a(i1, :) = a(i2, :)
a(i2, :) = rtmp
deallocate(rtmp)
tmp = b(i1)
b(i1) = b(i2)
b(i2) = tmp
end subroutine chgrow
!****************************************************************************
subroutine chgcol(m, n, a, ix, j1, j2)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), ix(n)
integer, intent(in) :: j1, j2
integer, allocatable :: rtmp(:)
integer :: tmp
allocate(rtmp(m))
rtmp = a(:, j1)
a(:, j1) = a(:, j2)
a(:, j2) = rtmp
deallocate(rtmp)
tmp = ix(j1)
ix(j1) = ix(j2)
ix(j2) = tmp
end subroutine chgcol
!****************************************************************************
subroutine setcol0(m, n, a, b, i)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), b(m)
integer, intent(in) :: i
integer :: ii, j, tmp
do ii = 1, m
if(ii == i)cycle
tmp = a(ii, i)
do j = 1, n
a(ii, j) = a(i, i)*a(ii,j) - tmp*a(i, j)
enddo
b(ii) = a(i, i)*b(ii) - tmp*b(i)
enddo
end subroutine setcol0
!****************************************************************************
subroutine normalize(m, n, a, x)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), x(m)
integer :: i, j
integer :: tmp, tmp2
l2:do i = 1, min(m, n)
if(a(i, i) /= 0)then
l1:do tmp2 = a(i, i), 1, -a(i, i)/abs(a(i, i))
do j = 1, n
if(mod(a(i, j), tmp2) /=0)cycle l1
enddo
if(mod(x(i), tmp2) /= 0)cycle l1
do j = 1, n
a(i, j) = a(i, j) / tmp2
enddo
x(i) = x(i) / tmp2
cycle l2
enddo l1
endif
enddo l2
end subroutine normalize
!****************************************************************************
subroutine normalize2(m, n, a, x)
!****************************************************************************
implicit none
integer, intent(in) :: m, n
integer, intent(inout) :: a(m, n), x(m)
integer :: i, j
integer :: tmp, tmp2
l2:do i = 1, m
tmp = maxval(abs(a(i,:)))
if(tmp /= 0)then
l1:do tmp2 = tmp, 1, -tmp/abs(tmp)
do j = 1, n
if(mod(a(i, j), tmp2) /=0)cycle l1
enddo
if(mod(x(i), tmp2) /= 0)cycle l1
do j = 1, n
a(i, j) = a(i, j) / tmp2
enddo
x(i) = x(i) / tmp2
cycle l2
enddo l1
endif
enddo l2
end subroutine normalize2
!****************************************************************************
subroutine print_mat(unit, m, n, a)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: unit, m, n, a(m, n)
integer :: i, j
do i = 1, m
write(unit, 1000)(a(i, j), j=1, n)
1000 format(100(1x, i4))
enddo
end subroutine print_mat
ソースコード2(ガウス・ジョルダン法の交代代入以降を行う)
!****************************************************************************
!
program msquare2
!
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
! 変数
integer :: m
! m : 魔方陣のサイズ(1辺に含まれる数字の個数)
integer, allocatable :: a(:,:), b(:), x(:), y(:,:)
! a(2*m+2,m**2) : 連立一次方程式の係数
! b(2*m+2) : 連立一次方程式の右辺
! x(m**2) : 解(1次元表示)
! y(m, m) : 解(2次元表示)
!
! 1次元配列xと魔方陣yの関係
! x(k) = y(i, j)
! k = (i-1)*m+j
! i = k/m+1
! j = mod(k,m)
integer, allocatable :: ix(:)
integer :: rank
! ix(m**2) : 列の入れ替え情報
! rank : 行列のランク
character(len=100) :: infile, ofile
! infile : msquare1の出力ファイル
integer :: i, j, io
write(nstde, *)'# infile, ofile=?'
read(*, *)infile, ofile
open(11, file = trim(infile), status = 'unknown', iostat = io)
if(io /= 0)then
write(nstde, *)'# can not open ' // trim(infile) //'.'
stop
endif
read(11, *) ! skip header
read(11, *)m
write(nstde, *)'# m=', m
allocate(a(2*m+2, m**2), b(2*m+2), x(m**2), ix(m**2))
read(11, *) ! skip header
read(11, *)rank
write(nstde, *)'# rank=', rank
read(11, *) ! skip header
do i = 1, 2*m+2
read(11, *)(a(i, j), j = 1, m**2)
enddo
write(nstde, *)'# --- a ---'
call print_mat(nstde, 2*m+2, m**2, a)
read(11, *) ! skip header
do i = 1, 2*m+2
read(11, *)b(i)
enddo
write(nstde, *)'# --- x ---'
call print_mat(nstde, 2*m+2, 1, b)
read(11, *) ! skip header
do i = 1, m**2
read(11, *)ix(i)
enddo
write(nstde, *)'# --- x ---'
call print_mat(nstde, m**2, 1, ix)
close(11)
call calc_x(2*m+2, m**2, rank, a, b, ix, x)
call check_x(m**2, x)
allocate(y(m, m))
do i = 1, m
do j = 1, m
y(i, j) = x((i-1)*m+j)
enddo
enddo
call check_y(m, y)
write(nstde, *)'# --- answer ---'
call print_mat(nstde, m, m, y)
open(12, file = trim(ofile), status = 'unknown', iostat = io)
if(io /= 0)then
write(nstde, *)'# can not open ' // trim(ofile) // '.'
stop
endif
call print_mat(12, m, m, y)
close(12)
end program msquare2
!****************************************************************************
subroutine calc_x(m, n, rank, a, b, ix, x)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, n, rank, a(m, n), b(m), ix(n)
integer, intent(out) :: x(n)
integer, allocatable :: x_tmp(:)
integer :: i, j, ii
! --- x_tmp(rank+1)~x_tmp(n)の生成(解が整数になるように適当に与える) ---
allocate(x_tmp(n))
x_tmp=0
ii = 0
do i = rank+1, n
ii = ii + 2
x_tmp(i) = ii
enddo
! --- x_tmp(1)~x_tmp(rank)の生成 ---
do i = 1, rank
x_tmp(i) = b(i)
do j = rank + 1, n
x_tmp(i) = x_tmp(i) - a(i, j) * x_tmp(j)
enddo
if(mod(x_tmp(i), a(i, i)) /= 0)then
write(nstde, *)'# not an integer.'
stop
endif
x_tmp(i) = x_tmp(i) / a(i, i)
enddo
! --- rank計算時に入れ替えていた変数を元に戻す ---
do i = 1, n
x(ix(i))=x_tmp(i)
enddo
end subroutine calc_x
!****************************************************************************
subroutine check_x(m, x)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, x(m)
integer :: i, j
do i = 1, m-1
do j = i+1, m
if(x(i) == x(j))then
write(nstde, *)i, j, x(i)
1000 format(' x(',i2,')=x(',i2,')=',i4)
endif
enddo
enddo
end subroutine check_x
!****************************************************************************
subroutine check_y(m, y)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: m, y(m, m)
integer :: i, j, tmp
write(nstde,*)'# --- sum ---'
do i = 1, m
write(nstde,*)sum(y(i, :))
enddo
do j = 1, m
write(nstde,*)sum(y(:, j))
enddo
tmp = 0
do i = 1, m
tmp = tmp+y(i, i)
enddo
write(nstde,*)tmp
tmp = 0
do i = 1, m
tmp = tmp+y(i, m-i+1)
enddo
write(nstde,*)tmp
end subroutine check_y
!****************************************************************************
subroutine print_mat(unit, m, n, a)
!****************************************************************************
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: unit, m, n, a(m, n)
integer :: i, j
do i = 1, m
write(unit, 1000)(a(i, j), j=1, n)
1000 format(100(1x, i4))
enddo
end subroutine print_mat
2014年5月29日木曜日
ロボット救出作戦
最近は災害現場でロボットの活躍が期待されている。というかもう活躍し始めているらしい。それを聞いて考えたのが、ロボットが途中で故障したらやっぱりロボットが救出に行くのだろうか、ということ。過酷な状況下では救出に行くロボットも故障するだろうから、一回の出動で救出出来ない場合もあるだろう。そんなことをあれこれ考えていたらちょっとしたパズルを思いついた。
(問題)
ある災害現場で、出動したロボット(No.0)が故障して止まってしまった。場所は出発点から距離Lの地点。ロボットには貴重な情報が入っているので別のロボットでけん引して回収したい。しかし、救出用ロボットもNo.0の所まで行って戻ってくるだけの堅牢さはなく、途中で故障してしまう。そこで、次々と救出用ロボットを繰り出して戻って来れるところまでけん引しては次のロボットに引き継ぐことにした(図1)。
救出用ロボットNo.1は距離a(<2L)しか走れないが、幸いなことに途中で技術が向上し、No.2はNo.1のb倍、No.3はNo.2のさらにb倍…というように、走行距離を増やしていける。さて、No.0をけん引して出発点まで戻って来れるのは何台めのロボットか。
(答え)
ロボットNo.kの最終位置をx(k)とする。x(k)は漸化式で表すことができる。
x(k)=2・x(k-1)-a・b^(k-1)
x(0)=L
なんか面倒な形になったが、ちょっと書き下してみるとこの漸化式は簡単に解くことができることがわかる。(面倒な人はWolfram先生に聞いてね!)
x(0)=L
x(1)=2・L-a
x(2)=2・(2・L-a)-a・b
x(3)=2・(2・(2・L-a)-a・b)-a・b^2
…
x(k)=2^k・L-a・(2^(k-1)+b・2^(k-2)+…b^(k-1))
よって、等比級数の公式を使って、
x(k)=L・2^k-a・(2^k - b^k)/(2-b)
となることがわかる。ここで、x(n)=0となるようなnを求めると、
n=log((a+(b-2)・L)/a)/log(b/2)
を得る。(ただしnは整数だから小数部分を切り上げた値が答えになる)
なお、図2はL=1の時のnのグラフをWolfram先生に描いてもらったもの。
…とまぁこんな感じ。別に意外な結果が出るわけではない。しいて言えば漸化式が簡単に解けるところが面白い。
(問題)
ある災害現場で、出動したロボット(No.0)が故障して止まってしまった。場所は出発点から距離Lの地点。ロボットには貴重な情報が入っているので別のロボットでけん引して回収したい。しかし、救出用ロボットもNo.0の所まで行って戻ってくるだけの堅牢さはなく、途中で故障してしまう。そこで、次々と救出用ロボットを繰り出して戻って来れるところまでけん引しては次のロボットに引き継ぐことにした(図1)。
 |
| 図1 ロボットの救出方法 |
救出用ロボットNo.1は距離a(<2L)しか走れないが、幸いなことに途中で技術が向上し、No.2はNo.1のb倍、No.3はNo.2のさらにb倍…というように、走行距離を増やしていける。さて、No.0をけん引して出発点まで戻って来れるのは何台めのロボットか。
ロボットNo.kの最終位置をx(k)とする。x(k)は漸化式で表すことができる。
x(k)=2・x(k-1)-a・b^(k-1)
x(0)=L
なんか面倒な形になったが、ちょっと書き下してみるとこの漸化式は簡単に解くことができることがわかる。(面倒な人はWolfram先生に聞いてね!)
x(0)=L
x(1)=2・L-a
x(2)=2・(2・L-a)-a・b
x(3)=2・(2・(2・L-a)-a・b)-a・b^2
…
x(k)=2^k・L-a・(2^(k-1)+b・2^(k-2)+…b^(k-1))
よって、等比級数の公式を使って、
x(k)=L・2^k-a・(2^k - b^k)/(2-b)
となることがわかる。ここで、x(n)=0となるようなnを求めると、
n=log((a+(b-2)・L)/a)/log(b/2)
を得る。(ただしnは整数だから小数部分を切り上げた値が答えになる)
なお、図2はL=1の時のnのグラフをWolfram先生に描いてもらったもの。
 |
| n=log((a+(b-2)・L)/a)/log(b/2)のグラフ。(ただしL=1) |
2014年5月23日金曜日
覆面算を計算するプログラムを作ってみた(CodeIQ)
CodeIQ 増井技術士事務所さんの問題(https://codeiq.jp/ace/thisweek_masuipeo/q860)に解答するため覆面算のプログラムを作った。Fortranで。
バッジ貰えたのでソースコード公開します:D
program Console1
implicit none
integer, parameter :: lm = 9
integer :: a(0:lm), l
integer :: i
write(*, 1000)
1000 format(' a d e i k l r s t w')
l = 0
do i = 0, lm
a(l) = i
call sub(lm, l, a)
enddo
end program Console1
recursive subroutine sub(lm, l, a)
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: lm, l, a(0:lm)
integer :: l1, a1(0:lm)
integer :: i, ii, p, q, r, s
if(l == lm)then
if(a(6) /= 0 .and. a(9) /= 0 .and. a(8) /= 0 .and. a(7) /= 0)then
p = a(6) * 1000 + a(2) * 100 + a(0) * 10 + a(1)
q = a(9) * 10000 + a(6) * 1000 + a(3) * 100 + a(8) * 10 + a(2)
r = a(8) * 1000 + a(0) * 100 + a(5) * 10 + a(4)
s = a(7) * 10000 + a(4) * 1000 + a(3) * 100 + a(5) * 10 + a(5)
if(s == p + q + r)then
write(nstde, 1000)(a(i), i = 0, lm)
1000 format(10(1x,i2))
endif
endif
else
l1 = l + 1
a1 = a
loop1: do i = 0, lm
a1(l1) = i
do ii = 0, l
if(a1(l1) == a1(ii))cycle loop1
enddo
call sub(lm, l1, a1)
enddo loop1
endif
end subroutine sub
問題ごとにプログラムを書き換える必要はあるけれど、再帰を使って割とシンプルにかけたと思う:)
バッジ貰えたのでソースコード公開します:D
program Console1
implicit none
integer, parameter :: lm = 9
integer :: a(0:lm), l
integer :: i
write(*, 1000)
1000 format(' a d e i k l r s t w')
l = 0
do i = 0, lm
a(l) = i
call sub(lm, l, a)
enddo
end program Console1
recursive subroutine sub(lm, l, a)
implicit none
integer, parameter :: nstde = 0
integer, intent(in) :: lm, l, a(0:lm)
integer :: l1, a1(0:lm)
integer :: i, ii, p, q, r, s
if(l == lm)then
if(a(6) /= 0 .and. a(9) /= 0 .and. a(8) /= 0 .and. a(7) /= 0)then
p = a(6) * 1000 + a(2) * 100 + a(0) * 10 + a(1)
q = a(9) * 10000 + a(6) * 1000 + a(3) * 100 + a(8) * 10 + a(2)
r = a(8) * 1000 + a(0) * 100 + a(5) * 10 + a(4)
s = a(7) * 10000 + a(4) * 1000 + a(3) * 100 + a(5) * 10 + a(5)
if(s == p + q + r)then
write(nstde, 1000)(a(i), i = 0, lm)
1000 format(10(1x,i2))
endif
endif
else
l1 = l + 1
a1 = a
loop1: do i = 0, lm
a1(l1) = i
do ii = 0, l
if(a1(l1) == a1(ii))cycle loop1
enddo
call sub(lm, l1, a1)
enddo loop1
endif
end subroutine sub
問題ごとにプログラムを書き換える必要はあるけれど、再帰を使って割とシンプルにかけたと思う:)
2014年5月22日木曜日
《チケットゴブル問題》をPerlで解いてみた(CodeIQ)
結城浩先生のチケットゴブル問題(https://codeiq.jp/ace/yuki_hiroshi/q863)を解いてみた。よく知られたアルゴリズム(貪欲法)に従えばもっと簡単に解けるとのことだけど、一応バッジ貰えたんでここに記録しておく。
1) 出発日の早い順にチケットを並べなおす。
2) 二枚のチケットの日程が包含関係にあるとき、日程の長い方の航空券を取り除く(全く同じ日程の場合は一方を取り除く)。
3) こうして得られたチケットの組を{(L1,R1),(L2,R2),...,(LN,RN)}と表すことにする。
Lk, Rkはそれぞれk番目のチケットの出発日、帰還日である。
4) (l1,r1)=(L1,R1)とする。
5) (lk,rk)=(LK,RK)とする。ただしKは、LK-1<=rk-1<LKを満たすように選ぶ。
5.の手順を繰り返すことにより得られたチケットの組{(l1,r1),...,(ln,rn)}は解の一つである。
上の手順で解の一つが求められるためには、
a){(L1,R1),...,(LN,RN)}の要素のみからなる解が存在する。
b)(L1,R1)を要素とする解が存在する。
c)ある解{(l1,r1),...,(ln,rn)}に対して、{(l1,r1),...,(lk-1,rk-1)}を含み、かつLK-1<=rk-1<LKを満たすような(LK,RK)を要素とするような解が存在する。
を証明すればよい。
a)の証明
ある解{(l1,r1),...,(ln,rn)}のk枚目のチケット(lk,rk)に対し、lk<l,r<rkとなるようなチケット(r,k)が存在するとする。{(l1,r1),..,(lk-1,rk-1),(l,r),(lk+1,rk+1),...,(ln,rn)}は日程が重複しないn枚のチケットからなるのでこれも解である。日程が包含関係にあるすべてのチケットに対しこの置き換えを行って得られる解は{(L1,R1),...,(LN,RN)}の要素のみからなる。//
以下、b)c)の証明ではa)の条件を満たす解のみについて考える。
b)の証明
(L1,R1)を含まないある解{(l1,r1),...,(ln,rn)}が存在するとする。1)2)より、L1<l1かつR1<r1である。解に含まれるチケット同士では日程は重複しないのでr1<l2,したがってR1<l2。
{(L1,R1),(l2,r2),...,(ln,rn)}は日程が重複しないn枚のチケットからなるのでこれも解である。//
c)の証明
(lk,rk)=(LK,RK)ならば証明終了。そうでない場合1)2)およびLK-1<=rk-1<LKより、LK<lkかつRK<rkである。解に含まれるチケット同士では日程は重複しないのでrk<lk+1,従ってRK<lk+1である。
{(l1,r1),...,(lk-1,rk-1),(LK,RK),(lk+1,rk+1),...,(ln,rn)}は日程が重複しないn枚のチケットからなるのでこれも解である。//
$infile = 'tickets.txt';
$ofilecsv = 'answer.csv';
$ofiletxt = 'answer.txt';
# $tk[$i][0] : 元データ
# $tk[$i][1] : 行先
# $tk[$i][2] : 出発日(Julian)
# $tk[$i][3] : 帰還日(Julian)
# $tk[$i][4] : 他の日程を包含する場合1, そうでない場合は0
open(INFILE, $infile) || die("# can not open $infile");
$i=0;
while(<INFILE>){
$tk[$i][0] = $_;
chomp($tk[$i][0]);
($tk[$i][1], $schedule) = split(/ /,$tk[$i][0]);
($date1, $date2) = split(/-/,$schedule);
($mm1, $dd1) = split(/\//, $date1);
($mm2, $dd2) = split(/\//, $date2);
$tk[$i][2]=jd($mm1, $dd1);
$tk[$i][3]=jd($mm2, $dd2);
$i++;
}
$nd = $i;
close(INFILE);
for ($i = 0; $i < $nd; $i++) {
$tk[$i][4] = 0;
for($j = 0; $j < $nd; $j++){
if($tk[$i][2] <= $tk[$j][2] &&
$tk[$i][3] >= $tk[$j][3]){
if($tk[$i][2] != $tk[$j][2] ||
$tk[$i][3] != $tk[$j][3] ||
$i > $j){
$tk[$i][4] = 1;
}
}
}
}
@tk2 = sort {$a->[4]<=>$b->[4] or $a->[2] <=> $b->[2]} @tk;
$tk3[0] = $tk2[0];
for($i = 1; $i < $nd; $i++){
if($tk2[$i][4] == 0){
if($tk2[$i][2] > $tk3[$#tk3][3]){
$tk3[$#tk3 + 1] = $tk2[$i];
}
}
}
open(OFILECSV, ">$ofilecsv") || die("# can not open $ofilecsv\n");
printf(OFILECSV "dest,jd1,jd2, flag, str\n");
for($i = 0; $i <= $#tk3; $i++){
printf(OFILECSV "%s, %d, %d, %d, %s\n",
$tk3[$i][1], $tk3[$i][2], $tk3[$i][3], $tk3[$i][4], $tk3[$i][0]);
}
@tk4 = sort {$a->[1] cmp $b->[1]} @tk3;
open(OFILETXT, ">$ofiletxt") || die("# can not open $ofiletxt\n");
printf(OFILETXT "%d", $#tk4 + 1);
for($i = 0; $i <= $#tk4; $i++){
printf(OFILETXT " %s", $tk4[$i][1]);
}
sub jd {
my (@dm, $jd, $mm, $dd, $i);
@dm = (31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31);
$jd = 0;
($mm, $dd) = @_;
for ($i = 1; $i < $mm; $i ++){
$jd = $jd + $dm[$i-1];
}
$jd = $jd + $dd;
return $jd;
}
1. アイディア
(証明に一部誤植がありました。すみません>結城先生)
複数存在する解のうちの一つを求める手順として以下を考えた。
1) 出発日の早い順にチケットを並べなおす。
2) 二枚のチケットの日程が包含関係にあるとき、日程の長い方の航空券を取り除く(全く同じ日程の場合は一方を取り除く)。
3) こうして得られたチケットの組を{(L1,R1),(L2,R2),...,(LN,RN)}と表すことにする。
Lk, Rkはそれぞれk番目のチケットの出発日、帰還日である。
4) (l1,r1)=(L1,R1)とする。
5) (lk,rk)=(LK,RK)とする。ただしKは、LK-1<=rk-1<LKを満たすように選ぶ。
5.の手順を繰り返すことにより得られたチケットの組{(l1,r1),...,(ln,rn)}は解の一つである。
上の手順で解の一つが求められるためには、
a){(L1,R1),...,(LN,RN)}の要素のみからなる解が存在する。
b)(L1,R1)を要素とする解が存在する。
c)ある解{(l1,r1),...,(ln,rn)}に対して、{(l1,r1),...,(lk-1,rk-1)}を含み、かつLK-1<=rk-1<LKを満たすような(LK,RK)を要素とするような解が存在する。
を証明すればよい。
a)の証明
ある解{(l1,r1),...,(ln,rn)}のk枚目のチケット(lk,rk)に対し、lk<l,r<rkとなるようなチケット(r,k)が存在するとする。{(l1,r1),..,(lk-1,rk-1),(l,r),(lk+1,rk+1),...,(ln,rn)}は日程が重複しないn枚のチケットからなるのでこれも解である。日程が包含関係にあるすべてのチケットに対しこの置き換えを行って得られる解は{(L1,R1),...,(LN,RN)}の要素のみからなる。//
以下、b)c)の証明ではa)の条件を満たす解のみについて考える。
b)の証明
(L1,R1)を含まないある解{(l1,r1),...,(ln,rn)}が存在するとする。1)2)より、L1<l1かつR1<r1である。解に含まれるチケット同士では日程は重複しないのでr1<l2,したがってR1<l2。
{(L1,R1),(l2,r2),...,(ln,rn)}は日程が重複しないn枚のチケットからなるのでこれも解である。//
c)の証明
(lk,rk)=(LK,RK)ならば証明終了。そうでない場合1)2)およびLK-1<=rk-1<LKより、LK<lkかつRK<rkである。解に含まれるチケット同士では日程は重複しないのでrk<lk+1,従ってRK<lk+1である。
{(l1,r1),...,(lk-1,rk-1),(LK,RK),(lk+1,rk+1),...,(ln,rn)}は日程が重複しないn枚のチケットからなるのでこれも解である。//
2. コード
#!/usr/bin/perl -w$infile = 'tickets.txt';
$ofilecsv = 'answer.csv';
$ofiletxt = 'answer.txt';
# $tk[$i][0] : 元データ
# $tk[$i][1] : 行先
# $tk[$i][2] : 出発日(Julian)
# $tk[$i][3] : 帰還日(Julian)
# $tk[$i][4] : 他の日程を包含する場合1, そうでない場合は0
open(INFILE, $infile) || die("# can not open $infile");
$i=0;
while(<INFILE>){
$tk[$i][0] = $_;
chomp($tk[$i][0]);
($tk[$i][1], $schedule) = split(/ /,$tk[$i][0]);
($date1, $date2) = split(/-/,$schedule);
($mm1, $dd1) = split(/\//, $date1);
($mm2, $dd2) = split(/\//, $date2);
$tk[$i][2]=jd($mm1, $dd1);
$tk[$i][3]=jd($mm2, $dd2);
$i++;
}
$nd = $i;
close(INFILE);
for ($i = 0; $i < $nd; $i++) {
$tk[$i][4] = 0;
for($j = 0; $j < $nd; $j++){
if($tk[$i][2] <= $tk[$j][2] &&
$tk[$i][3] >= $tk[$j][3]){
if($tk[$i][2] != $tk[$j][2] ||
$tk[$i][3] != $tk[$j][3] ||
$i > $j){
$tk[$i][4] = 1;
}
}
}
}
@tk2 = sort {$a->[4]<=>$b->[4] or $a->[2] <=> $b->[2]} @tk;
$tk3[0] = $tk2[0];
for($i = 1; $i < $nd; $i++){
if($tk2[$i][4] == 0){
if($tk2[$i][2] > $tk3[$#tk3][3]){
$tk3[$#tk3 + 1] = $tk2[$i];
}
}
}
open(OFILECSV, ">$ofilecsv") || die("# can not open $ofilecsv\n");
printf(OFILECSV "dest,jd1,jd2, flag, str\n");
for($i = 0; $i <= $#tk3; $i++){
printf(OFILECSV "%s, %d, %d, %d, %s\n",
$tk3[$i][1], $tk3[$i][2], $tk3[$i][3], $tk3[$i][4], $tk3[$i][0]);
}
@tk4 = sort {$a->[1] cmp $b->[1]} @tk3;
open(OFILETXT, ">$ofiletxt") || die("# can not open $ofiletxt\n");
printf(OFILETXT "%d", $#tk4 + 1);
for($i = 0; $i <= $#tk4; $i++){
printf(OFILETXT " %s", $tk4[$i][1]);
}
sub jd {
my (@dm, $jd, $mm, $dd, $i);
@dm = (31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31);
$jd = 0;
($mm, $dd) = @_;
for ($i = 1; $i < $mm; $i ++){
$jd = $jd + $dm[$i-1];
}
$jd = $jd + $dd;
return $jd;
}
2014年4月30日水曜日
スピンスピン
僕は学生時代工学部で海洋環境の数値シミュレーションをやっていたのだが(というか今もやってる)、取り組みが始まったばかりで学科内には地球流体の専門家の先生がいなかったので、地球物理学のK先生の授業を他学部聴講で聞きに行ったことがある。講義の中でいろいろな実験のデモやビデオを見せていただいたが、そのなかにエクマンパンピングの実験があった。回転水槽の回転数を変化させたときに、水槽の水の回転が水槽の回転に追随していく様子を実際に測ってみよう、というものだ。
当時は内容がよく理解できなくて、結局この実験のレポートは出さなかったのだけど、期末になったらちゃんと単位がついていた。せっかく他学部から聞きに来てくれたので、ということでおまけしてくださったとのこと。その後、自分でちゃんとやり直してみようと思いつつ、気が付いたらウン十年もたってしまった。
…というわけで、再履修のつもりでエクマンパンピングの実験をやってみることにした。
とりあえず今回は水槽の性能などを確かめるための予備実験。準備するものは以下の通り。
当時は内容がよく理解できなくて、結局この実験のレポートは出さなかったのだけど、期末になったらちゃんと単位がついていた。せっかく他学部から聞きに来てくれたので、ということでおまけしてくださったとのこと。その後、自分でちゃんとやり直してみようと思いつつ、気が付いたらウン十年もたってしまった。
…というわけで、再履修のつもりでエクマンパンピングの実験をやってみることにした。
とりあえず今回は水槽の性能などを確かめるための予備実験。準備するものは以下の通り。
- 回転台:レコードプレーヤーを使用する。回転数を変えられるので便利。(電動ろくろは騒音が出るので使用を見送った)
- 水槽:円筒形のガラス食器を使用する。ターンテーブルの真ん中のでっぱりの邪魔にならないよう土台を別途用意する。
- ストップウォッチ:ラップ・スプリット計測が可能でメモリー付きのもの。
- 浮子:水の回転速度を測るのに使う。今回はアルミホイルを、沈んでしまわないように空気がたまるような形にして使った。
手順は以下の通り。
- 水槽に水を張り、浮子を浮かべる。
- 回転台の上に置いて45回転/分で回転させる。
- 浮子が1周するのにかかる時間(回転周期)を測る(ちゃんと計れているかどうか確認するために複数回測る)
- 途中で回転数を33 1/3回転に切り替える。
- 浮子の回転周期を測り続ける。
そして得られた結果が下のグラフだ。ストップウォッチで正しく周期を測るのは難しいが、一応なんとかなりそうだ。なれればもっと正しく測れそうな気もする。
 |
図1 : レコードプレーヤーの回転数設定を45回転/分から33 1/3回転/分に切り変えた時の水の回転周期の変化。青が回転周期の生の値、オレンジはその5区間移動平均、黄と緑の線は45回転/分、33 1/3回転/分にセットした時の実際の回転周期。
せっかくなので、スピンダウンタイム(水の回転が水槽の回転になじむまでの時間スケール)についてざっくり答え合わせをしてみよう。水槽の深さをH、回転の角速度をΩ、水の動粘性係数をνとすると、水槽に対する水の総体的な回転数が1/e (=1/2.71828...)になるのにかかる時間スケール(スピンダウンタイム)は以下の式で与えられる。
T=fδ_e/2H
ただしfはコリオリパラメータで、
f=2Ω
δ_eは水底のエクマン境界層の厚さで、
δ_e=√(2ν/f)
である。(式の導出等はは京都大学の久保川先生のテキスト参照のこと)
ここで、ν~1.0e-6 m^2 s^-1, Ω~8.4 rad s^-1, H~0.1 mとして計算するとT~48 sを得る。上のグラフでは横軸を測定番号にしているので分かりにくいけれども、だいたい30~40秒くらいで水の回転が水槽の回転になじんでいる。適当にやって適当に検算した割にはまぁいい線行っているのではないか。
とりあえず今回はこんなところ。時間をみてまたやってみよう。
2014年4月5日土曜日
水の温度を測る(氷水の温度を測る の続き)
予告通り?またしても水の温度を測る実験をやってみた。今回は、4℃の氷水とほぼ室温の水を用意して、温度計を氷水で冷やしておいたあと、室温の水に入れ、時々刻々の読みの変化を記録した。
 |
| Fig.1 氷水の温度 |
氷水の温度はこの通り(Fig.1)。うっかり冷やしすぎたのであとから少し水を足して調節した。
 |
| Fig.2 実験風景(再現) |
室温の水を用意するために、丼(Fig.2)に水を張って数時間放置した。実験前に予備的に測ってみたところ室温よりは1℃ほど低かったようだが、実験に支障をきたすほどの急な温度変化はないだろう。で、結果は以下の通り(Fig.3)。
 |
| Fig.3 実験結果 |
最初の100秒のデータを使って、ΔT=C・exp(-αt)にフィッティングしてみたところ、α≒0.046を得た。これは前回の結果に近い。log(10)/α≒50だから、50秒待てば温度計の読みと水温の差は最初の1/10になるということだ。ただし、前回もそうだったが指数関数によるフィッティングでは最初の10秒の急激な変化をぜんぜん再現できないので、実際には20秒程度まてばOKなんじゃないだろうか。
というわけで、棒温度計の特性はだいたいわかってきたけど、単純な指数関数による近似では限界があるなあ。
2014年4月3日木曜日
氷水の温度を測る
温度を測るシリーズ、いったん終了と見せかけて実はしつこく続いていたのだった。
お湯を冷やす(2)の中で使った式に現れる定数のうち,温度計の応答速度を表す定数であるαは温度を一定とした水の温度を測ることで調べることができる。というわけで、氷水を入れたガラス瓶を用意してほぼ常温を示している温度計を突っ込み,10秒ごとにその温度を測ってみた。
ポットを使うことも考えたけど,温度を測るために口をあけていると結構温度が下がるので,ここでは氷水を使うことにした.潜熱による熱容量の大きさがバッファになると期待.あとやってみて気が付いたのだけど,水の比重は4℃で最低になるので,うまく水と氷の量を調節して,かつかきまぜたりしなければ,底に近い所の水は常に4℃付近になる(冬の湖と同じ).
ガラス瓶の質量は135g(前回使用したのと同じビンなんだけど計るたびに値が微妙に変わるのは秤の精度がそこまでないため),実験は3回行い,水+氷の量はrun1で155g, run2,3で145g(同じ水+氷を続けて使用).室温は約22℃だった.
というわけで結果がこちら(Fig.1).0秒では温度計はほぼ室温を示していたのは確認したのだが,正確な値を記録していなかったのでプロットはしていない.
run2だけ途中4℃からじわじわ温度が下がっているけれど,これは氷の量が多く,しかも途中温度計を動かしてしまい水が混ざってしまったためだろう.今は温度計の支持具が無いので手で持って測っている.これだと温度計の位置が安定しないし持ち替えるときなどに意図せずかきまぜてしまうので,次回は番線か何かで支持具を作ってみようと思う.
さて,ここで定数αを求める為,run1と3について,LibreOfficeの機能を使って実験結果を指数関数でフィッティングしてみた結果がこちら(Fig2, 3).グラフの横軸は経過時間(秒),縦軸は温度計の読みと水温(4℃)との差(℃)で,前回の仮定が正しければf(t)=A・exp(-αt)にフィットさせることができるはずである.
ちっとも合わない(-_-;とりあえずαの値は,全データを使用した時0.016 1/s,最初の1分のデータを使用した時0.04 1/s程度であったが,おおよその目安にはなるものの胸を張ってあってますとは言い難いなあ.ちなみにα=0.04とは,誤差が測り始めの1/10になるのに約1分かかるということを表している.
ところで,実験のあとで気が付いたけど,温度計の方を加熱あるいは冷却しておいて,常温に戻る様子を観察するほうが実験としては簡単だったかもしれない.というか次回にでもやってみよう.(←まだ続くのか
お湯を冷やす(2)の中で使った式に現れる定数のうち,温度計の応答速度を表す定数であるαは温度を一定とした水の温度を測ることで調べることができる。というわけで、氷水を入れたガラス瓶を用意してほぼ常温を示している温度計を突っ込み,10秒ごとにその温度を測ってみた。
ポットを使うことも考えたけど,温度を測るために口をあけていると結構温度が下がるので,ここでは氷水を使うことにした.潜熱による熱容量の大きさがバッファになると期待.あとやってみて気が付いたのだけど,水の比重は4℃で最低になるので,うまく水と氷の量を調節して,かつかきまぜたりしなければ,底に近い所の水は常に4℃付近になる(冬の湖と同じ).
ガラス瓶の質量は135g(前回使用したのと同じビンなんだけど計るたびに値が微妙に変わるのは秤の精度がそこまでないため),実験は3回行い,水+氷の量はrun1で155g, run2,3で145g(同じ水+氷を続けて使用).室温は約22℃だった.
というわけで結果がこちら(Fig.1).0秒では温度計はほぼ室温を示していたのは確認したのだが,正確な値を記録していなかったのでプロットはしていない.
 |
| Fig.1 氷水の温度を測った結果 |
run2だけ途中4℃からじわじわ温度が下がっているけれど,これは氷の量が多く,しかも途中温度計を動かしてしまい水が混ざってしまったためだろう.今は温度計の支持具が無いので手で持って測っている.これだと温度計の位置が安定しないし持ち替えるときなどに意図せずかきまぜてしまうので,次回は番線か何かで支持具を作ってみようと思う.
さて,ここで定数αを求める為,run1と3について,LibreOfficeの機能を使って実験結果を指数関数でフィッティングしてみた結果がこちら(Fig2, 3).グラフの横軸は経過時間(秒),縦軸は温度計の読みと水温(4℃)との差(℃)で,前回の仮定が正しければf(t)=A・exp(-αt)にフィットさせることができるはずである.
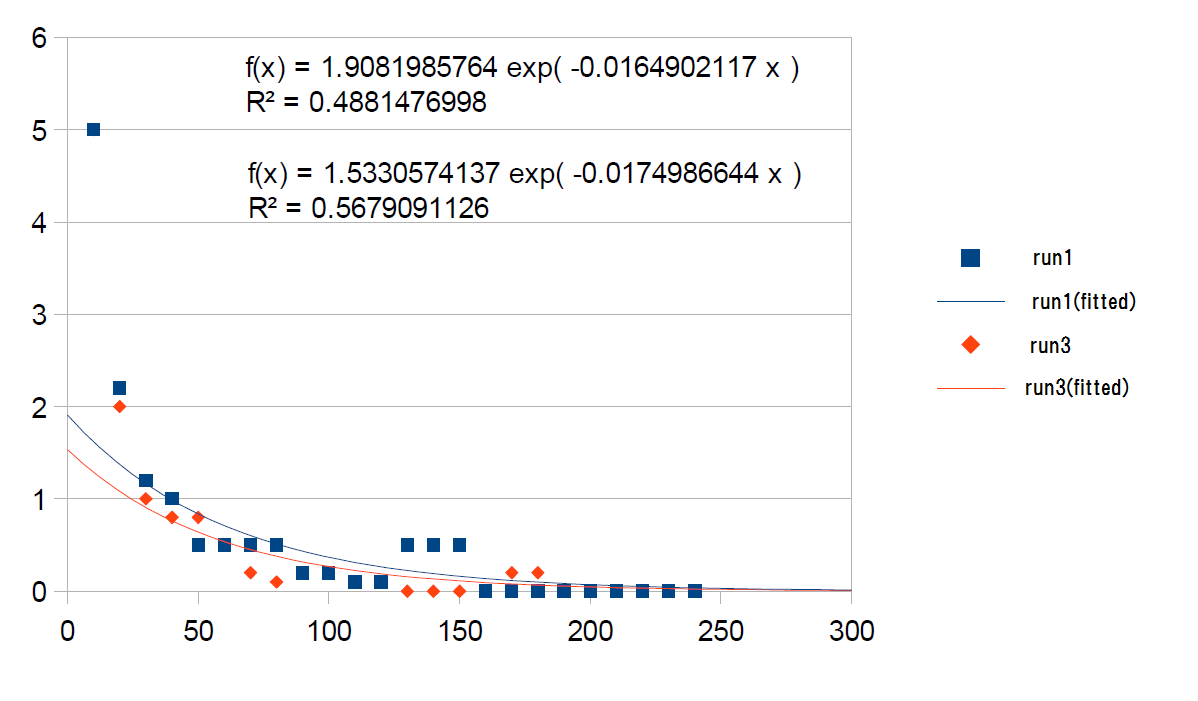 |
| Fig.2 指数関数によるフィッティングの結果(全データ使用) |
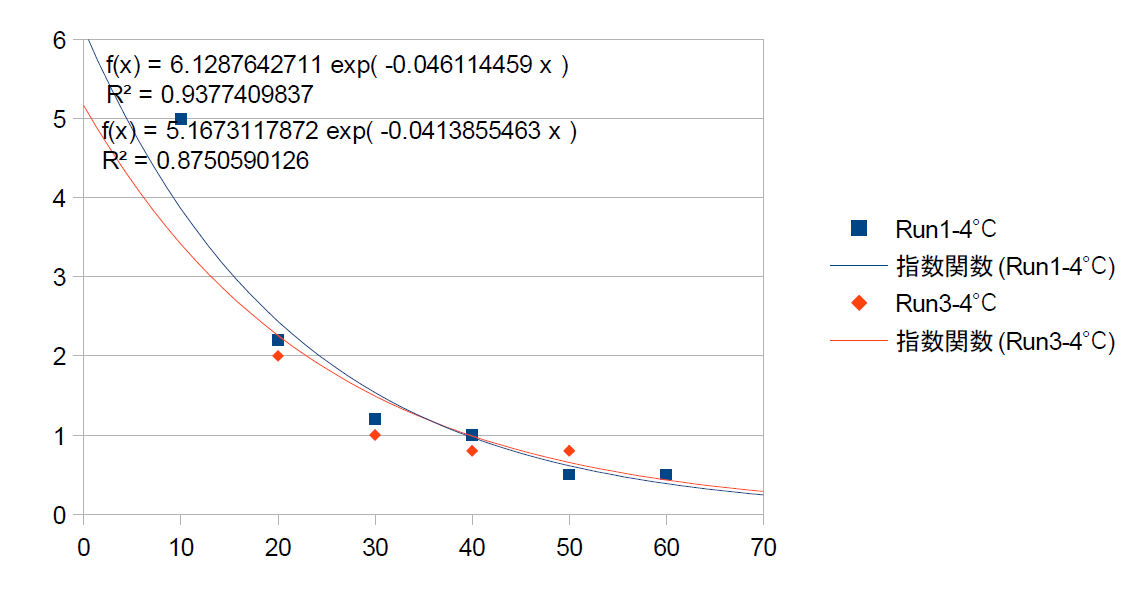 |
| Fig.3 指数関数によるフィッティングの結果(開始後60秒までのデータのみ使用) |
ちっとも合わない(-_-;とりあえずαの値は,全データを使用した時0.016 1/s,最初の1分のデータを使用した時0.04 1/s程度であったが,おおよその目安にはなるものの胸を張ってあってますとは言い難いなあ.ちなみにα=0.04とは,誤差が測り始めの1/10になるのに約1分かかるということを表している.
ところで,実験のあとで気が付いたけど,温度計の方を加熱あるいは冷却しておいて,常温に戻る様子を観察するほうが実験としては簡単だったかもしれない.というか次回にでもやってみよう.(←まだ続くのか
2014年3月17日月曜日
お湯を冷やす(2)
せっかくなので前回の問題を解いてみた.
容器にお湯を入れ,棒温度計で測ることにする.
dT/dt=-α(T-T_w)
dT_w/dt=-β(T_w-Ta)
ばねます系と同じ1階の線形連立常微分方程式.これを解くと,
T=T_a + ((T_0-T_a)-(α/(α-β))(T_w0-Ta))exp(-αt)+(α/(α-β))(T_w0-Ta)exp(-βt)
T_w=T_a+(T_w0-Ta)exp(-βt)
を得る.(α=βの時は解はこれとは異なる形になるのだけれど,そもそもα≦βだと温度計が水温の変動に追随しきれなくなってナンセンスなのでここでは考えない)
Tの式を見ると,定数の第一項,速やかに0に収束する第2項,緩やかに0に収束する第3項の和になっている.また,第3項はT_wの式の定数倍になっている.これらのことから,温度計の読みはまず急激に水温に近づき,その後水温に追随して室温に近づいていく,というおおまかな挙動が分かる.
α=0.1 sec^-1, β=0.001 sec^-1, T_0=15.0℃, T_a=11.0℃, T_w0=77.0℃ としてグラフを書いてみるとFig.1のようになる.(赤が水温,青が温度計の読み)
うむ,前回の実験とよく似た曲線が得られている.まぁほんとは実験にフィットさせて初めて説明できたってことになるんだけど,そのためにはα,βを求める実験やらなきゃなのでとりあえずここまで.
なお,α>>βと仮定すると,α/(α-β)~1よりTの式は
T=T_a+(T_0-T_w0)exp(-αt)+(T_w0-T_a)exp(-βt)
となる.正確さには欠けるけれどもグラフの雰囲気をつかむにはこちらの方がいいかも.
追記:こちらのまとめ「「温度計の示度は気温の変化に遅れて指数関数的に平衡値に近づく」の?」の後ろの方に任意の水温変化に対する温度計の応答の解が紹介されている.
容器にお湯を入れ,棒温度計で測ることにする.
- 気温をT_a, 初期水温をT_w0, 温度計の初期温度をT_0とする.
- 水の熱容量が温度計の熱容量にくらべ十分大きく,温度計で測ることにより水温が変化することはないものとする.
- お湯と空気,お湯と温度計の間の熱伝達の速度はそれぞれ両者の温度差に比例すると仮定する.
dT/dt=-α(T-T_w)
dT_w/dt=-β(T_w-Ta)
ばねます系と同じ1階の線形連立常微分方程式.これを解くと,
T=T_a + ((T_0-T_a)-(α/(α-β))(T_w0-Ta))exp(-αt)+(α/(α-β))(T_w0-Ta)exp(-βt)
T_w=T_a+(T_w0-Ta)exp(-βt)
を得る.(α=βの時は解はこれとは異なる形になるのだけれど,そもそもα≦βだと温度計が水温の変動に追随しきれなくなってナンセンスなのでここでは考えない)
Tの式を見ると,定数の第一項,速やかに0に収束する第2項,緩やかに0に収束する第3項の和になっている.また,第3項はT_wの式の定数倍になっている.これらのことから,温度計の読みはまず急激に水温に近づき,その後水温に追随して室温に近づいていく,というおおまかな挙動が分かる.
α=0.1 sec^-1, β=0.001 sec^-1, T_0=15.0℃, T_a=11.0℃, T_w0=77.0℃ としてグラフを書いてみるとFig.1のようになる.(赤が水温,青が温度計の読み)
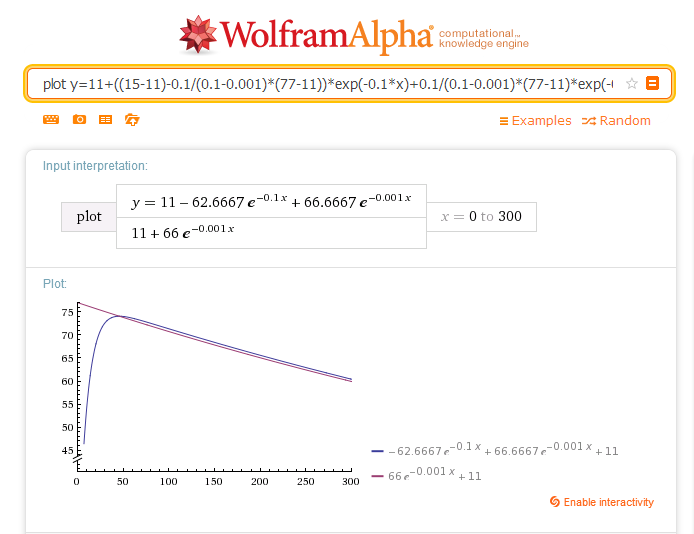 |
| Fig.1 |
うむ,前回の実験とよく似た曲線が得られている.まぁほんとは実験にフィットさせて初めて説明できたってことになるんだけど,そのためにはα,βを求める実験やらなきゃなのでとりあえずここまで.
なお,α>>βと仮定すると,α/(α-β)~1よりTの式は
T=T_a+(T_0-T_w0)exp(-αt)+(T_w0-T_a)exp(-βt)
となる.正確さには欠けるけれどもグラフの雰囲気をつかむにはこちらの方がいいかも.
追記:こちらのまとめ「「温度計の示度は気温の変化に遅れて指数関数的に平衡値に近づく」の?」の後ろの方に任意の水温変化に対する温度計の応答の解が紹介されている.
2014年3月15日土曜日
お湯を冷やす
いろいろやってみて思ったのだが、どうも温度計の目盛りを読む前に温度そのものが変化してしまっているっぽい。そこで、実際温度計の読みが時間がたつにつれてどのように変化するか調べてみた。
ガラス瓶(132.5g)に100gの湯を入れ、温度計を挿入してから10秒ごとに値を読み取った。
ちなみに気温は11.0℃、水道水温は9.0℃だった。ちょっと寒い。
結果はFig.1の通り。水温は1分当たり3度くらい下がる。一方で温度計が水温になじむまでには3~40秒かかっている。
 |
| Fig.1 |
時系列の途中を取り出して線形近似し、外挿によって元の水温を推定してみると約77.1℃になった(Fig.2)。この値は温度計の最大の読み取り値と比較すると2℃ほど高い。
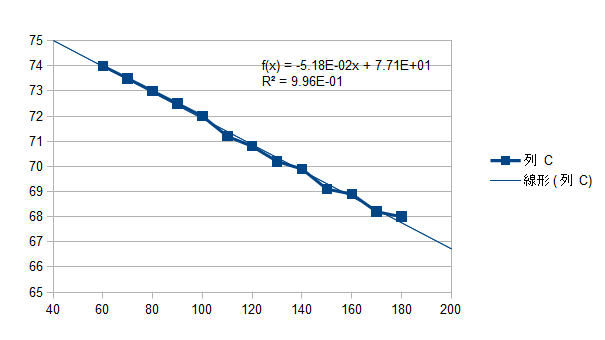 |
| Fig.2 |
というわけで、温度計が水温に追随するのに時間がかかり、その間に起こる温度変化が無視できないことが、これまでの実験の誤差の主要な原因の一つらしい、ということが分かった。
誤差を減らすには上でやったように複数回計って外挿してやればよいわけだけど、昔理科の実験でそんなめんどくさい事をやった記憶はないなあ。もっと手っ取り早い方法はないのかな。(対象の数だけ温度計を複数用意して予熱しておくとか…?)
2014年3月14日金曜日
水と湯を混ぜる(2)
容器を通して熱が逃げるのを抑制するためにポットの中で水を混ぜてみた.
ちなみに気温15℃, 水温(蛇口)10℃,熱量は0℃基準.
ところで,「中学校理科の授業記録」というウェブサイトを見つけた.水とお湯を混ぜる実験が紹介されている.
ここでも理論値と実験値はよく一致している(1℃以内)…なんでうちの実験はだめなんだー
ちなみに気温15℃, 水温(蛇口)10℃,熱量は0℃基準.
やっぱり誤差が2℃近くある.初回は3~7℃程度誤差があったので全く進歩していないわけではないけれども.
ところで,「中学校理科の授業記録」というウェブサイトを見つけた.水とお湯を混ぜる実験が紹介されている.
ここでも理論値と実験値はよく一致している(1℃以内)…なんでうちの実験はだめなんだー
2014年3月13日木曜日
水と湯を混ぜる
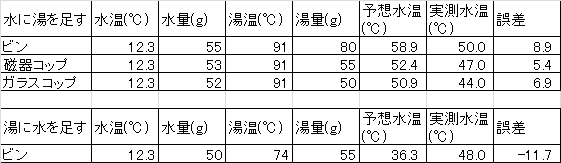
おちさんは実験にガラス容器を使ってうまくいったとのことだったので,容器を変えると結果が改善されるかどうか,昨日の実験1をやり直してみた.用意したのはガラスビン(左,135g),脚付きのガラスコップ(中,218g),前回も使用した磁器製のマグカップ(182g).
容器に水を入れておきあとからポットのお湯を足してみた.また,ガラスビンについては「先に湯を入れておいて後から水を足す」もやってみた.
結果は…
かえって誤差が増えてる(x_x).どうやら僕の実験で誤差が生じる理由は別の所にありそうだ.
ところで,昨日は秤に問題があるかも,と書いたけれどもメインの理由ではないかもしれない.もし秤の値のばらつきが原因だとしたら,誤差は0を中心にばらつくはずだが,水に湯を足す場合常に予想水温>実測水温となっている.
2014年3月12日水曜日
0℃の氷100gと100℃のお湯100gを混ぜると何度になるか?の続き
はじめに
0℃の氷100gと100℃のお湯100gを混ぜると何度になるか?という問題について,しばらく前にやってtwitterでつぶやいたのだけど(http://togetter.com/li/630940),おちさんのブログ(http://www.02320.net/2014/02/16/mixing_ice_and_hot_water/, http://www.02320.net/2014/02/18/pouring_hot_water_on_ice/)を見てもうすこしまともに考察したいと思ってやり直してみた.ただ,相変わらず道具がしょぼいので大した進歩がないことはご愛嬌.方法
当日の室温は15.8℃,水道水の水温は11.2℃.使用機材は磁器のマグカップ(135g),クッキング用のばね秤と棒温度計.お湯は沸かした後ポットに保存.そのため湯の温度は100℃ではなく91~93℃くらい.
氷の温度は棒温度計ではうまく測れない.うちの冷凍庫の性能はカタログ値で-18℃以下ということなので,取り出したばかりの氷なら-18℃くらいとみてよいだろう.
水の比熱は1cal g^-1 K^-1,氷の比熱は0.5cal g^-1 K^-1,融解熱は79cal g^-1とした.
実験は以下の4通り行った.
実験1. 適当に決めた水温,水量のことなる二種類の水を混ぜる.
実験2. 冷凍庫から出したての氷にポットのお湯を掛ける.
実験3. マグカップのお湯に室内に冷蔵庫から出したての氷を入れる.
実験4. マグカップのお湯に室内に(30分くらい?)放置していた氷を入れる.
結果
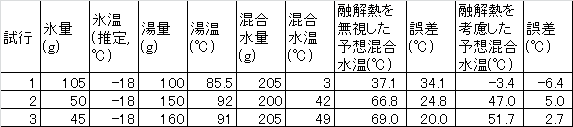
実験1
分量を変えて4回行い,式(1)(後述)による予想水温と比較した.結果は以下の通り.
前回もそうだったがおちさんの結果に比べて誤差がかなりでかい.原因については後で考えることにしてとりあえずその程度の誤差のある実験だということで(前回も同じことを書いたような…進歩なし)
実験2
温度と分量を変えて3回行った.
お湯と氷がそれぞれ100gじゃないのは,一つにはマグカップでは水の量の調節が難しいこと,氷1個あたりの量が製氷皿の形状であらかじめ決まっていること,等量にすると溶けるのに時間がかかってしまうこと,などの理由による.
お湯と氷がそれぞれ100gじゃないのは,一つにはマグカップでは水の量の調節が難しいこと,氷1個あたりの量が製氷皿の形状であらかじめ決まっていること,等量にすると溶けるのに時間がかかってしまうこと,などの理由による.
当たり前だが融解熱を無視すると全然合わない:D
試行1では融解熱を考慮した場合の予想水温がマイナスになっているが,これは熱量が足りないのに無理やり全部溶けるとして計算したため.実際,試行1ではかなり長い間かきまぜないと全ての氷が溶けなかった.最終的に溶けたのはかきまぜているあいだに熱の出入りがあったためだろう.
実験3
温度と分量を変えて2回行った.予想水温については実験2と同じ.
実験2より誤差は小さめになったが理由は不明.
実験4
試行回数がだんだん減ってることには目をつぶってほしい(-_-;というか,実はこれは偶々室内に氷を放置してたことに気が付いたのでやってみただけ…
氷の温度はとりあえず0℃としたが実際にはもっと低いだろう.
考察
前回に引き続き,氷とお湯を混ぜる問題で,融解熱を無視できないことが確認できた.おちさん風に言えば「0℃の氷1gは-80℃の水と同じ」だから当然の結果だ.
実験1の段階ですでに誤差が5℃ほどあるのはなんでかというと,まずは秤の誤差が大きい.というのも,うちのばね秤はフリクションがでかいので,叩いて測りなおすと10gくらい値が変わることなんて日常茶飯事なのだ(あっでも料理作るのには重宝してます念の為).
ちなみに,質量M_1, 水温T_1の水と質量M_2,水温_T2の水を混ぜたときの温度をTとすると,
だから,質量と水温の測定に起因する誤差を
ちなみに,質量M_1, 水温T_1の水と質量M_2,水温_T2の水を混ぜたときの温度をTとすると,
だから,質量と水温の測定に起因する誤差を
で見積もることができる.実験1-1の場合,仮にM_1の測定時の誤差が10gだったとするとそれに起因するTの誤差は2℃程度ということになる.M_2にも同程度の誤差が含まれているとすれば併せて4℃くらいずれてもおかしくない(もちろんお互いに誤差を打ち消しあう可能性もあるけど).
また,開放系で実験していることの影響も無視できないだろう.今回気になったのはマグカップとの熱のやり取り.陶磁器の熱容量は(理科年表のガラスや岩石の値から類推するに)水の10%程度はあるだろうし,実験の最中に結構マグカップの温度も変化していた.
実験3でお湯の温度が低いのは,ポットから移す時に温度が下がったから.実験2ではポットの中で湯の温度を測ってからマグカップに注いでいるので,実験3より精度が低くなるのではないかと予想した.実際誤差は大きかったが,水温や質量を揃えていないのでほんとにそれが原因と言っていいのかどうかよくわからない.
なお,結露も実験の結果を大きく左右するけれども,今回は(実験2-1を除き)水温が全体に高めだったためか,結露はほとんど見られなかった.
おわりに
次はまじめにやる.
登録:
投稿 (Atom)